LeetCode刷题笔记(五): 搜索
搜索算法主要包括深度优先搜索和广度优先搜索。
一、深度优先搜索
算法介绍：深度优先搜索(depth-first search，DFS)在搜索到一个新的节点时，立即对该新节点进行遍历；因此遍历需要用先入后出的栈(stack)来实现，也可以通过与栈等价的递归来实现。对于树结构而言，由于总是对新节点调用遍历，因此看起来是向着“深”的方向前进。
1
2
3
4
51
/ \
2 3
/
4考虑上面这棵简单的树，深度优先搜索的顺序为1->2->4->3。
补充：
- 深度优先搜索可以用来检测环路：记录每个遍历过的节点的父节点，若一个节点被再次遍历且父节点不同，则说明有环。我们也可以用之后会讲到的拓扑排序判断是否有环路，若最后存在入度不为零的点，则说明有环。
- 有时我们可能会需要对已经搜索过的节点进行标记，以防止在遍历时重复搜索某个节点，这种做法叫做状态记录或记忆化(memoization)。
题目一：岛屿的最大面积
给定一个二维的0-1矩阵，其中0表示海洋，1表示陆地。单独的或相邻的陆地可以形成岛屿，每个格子只与其上下左右四个格子相邻。求最大的岛屿面积。解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
vector<pair<int, int>> island;
vector direction = {0, 1, 0, -1, 0};
int maxArea = 0;
for (int i = 0; i < grid.size(); ++i) {
for (int j = 0; j < grid[0].size(); ++j) {
int localArea = 0;
if (grid[i][j] == 1) {
island.push_back({i, j});
grid[i][j] = 0;
while (!island.empty()) {
auto [h, l] = island.back();
island.pop_back();
++localArea;
for (int k = 0; k < 4; ++k) {
int newH = h + direction[k], newL = l + direction[k + 1];
if (newH >= 0 && newH < grid.size() && newL >= 0 && newL < grid[0].size() && grid[newH][newL] == 1) {
island.push_back({newH, newL});
grid[newH][newL] = 0;
}
}
}
}
maxArea = max(maxArea, localArea);
}
}
return maxArea;
}
};解答二(递归解法)：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int maxArea = 0;
for (int i = 0; i < grid.size(); ++i) {
for (int j = 0; j < grid[0].size(); ++j) {
if (grid[i][j] == 1)
maxArea = max(maxArea, dfs(grid, i, j));
}
}
return maxArea;
}
private:
int dfs(vector<vector<int>>& grid, int i, int j) {
if (i < 0 || i >= grid.size() || j < 0 || j >= grid[0].size() || grid[i][j] == 0) {
return 0;
}
grid[i][j] = 0;
return 1 + dfs(grid, i + 1, j) + dfs(grid, i - 1, j) + dfs(grid, i, j + 1) + dfs(grid, i, j - 1);
}
};提示：非常标准的深度搜索题，要记得做状态记录。
题目二：省份数量
给定一个二维的0-1矩阵，如果第(i, j)位置是1，则表示第i个城市和第j个城市处于同一城市圈。已知城市的相邻关系是可以传递的，即如果a和b相邻，b和c相邻，那么a和c也相邻，换言之这三个城市处于同一个城市圈之内。求一共有多少个城市圈。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
void dfs(vector<vector<int>> &isConnected, int i, vector<bool> &visited) {
visited[i] = true;
for (int j = 0; j < isConnected.size(); ++j) {
if (isConnected[i][j] == 1 && !visited[j]) {
dfs(isConnected, j, visited);
}
}
}
int findCircleNum(vector<vector<int>> &isConnected) {
int n = isConnected.size(), count = 0;
vector<bool> visited(n, false);
for (int i = 0; i < n; ++i) {
if (!visited[i]) {
dfs(isConnected, i, visited);
++count;
}
}
return count;
}
};提示：使用状态数组来记录状态。
题目三：太平洋大西洋水流问题
给定一个二维的非负整数矩阵，每个位置的值表示海拔高度。假设左边和上边是太平洋，右边和下边是大西洋，求从哪些位置向下流水，可以流到太平洋和大西洋。水只能从海拔高的位置流到海拔低或相同的位置。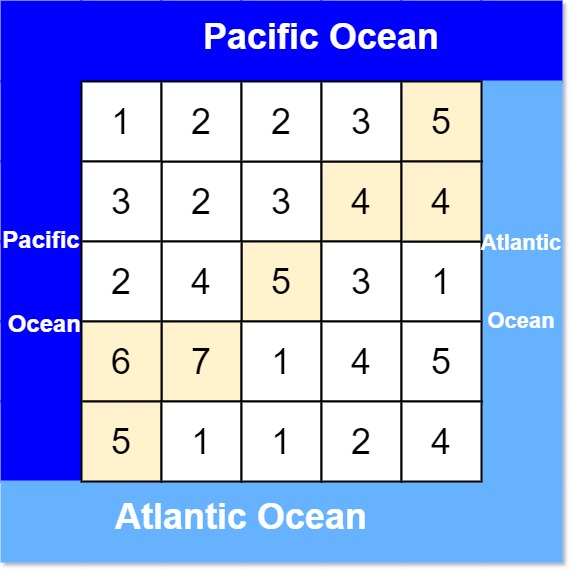
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38class Solution {
private:
vector<int> directions = {-1, 0, 1, 0, -1};
public:
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
int m = heights.size();
int n = heights[0].size();
vector<vector<int>> res;
vector<vector<bool>> canReachP(m, vector<bool>(n, false));
vector<vector<bool>> canReachA(m, vector<bool>(n, false));
for (int i = 0; i < m; ++i) {
flow(heights, canReachP, i, 0);
flow(heights, canReachA, i, n - 1);
}
for (int i = 0; i < n; ++i) {
flow(heights, canReachP, 0, i);
flow(heights, canReachA, m - 1, i);
}
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (canReachA[i][j] && canReachP[i][j])
res.push_back({i, j});
}
}
return res;
}
void flow(vector<vector<int>>& heights, vector<vector<bool>>& canReach, int l, int c) {
if (canReach[l][c]) return;
canReach[l][c] = true;
for (int i = 0; i < 4; ++i) {
int x = l + directions[i], y = c + directions[i + 1];
if (x >= 0 && x < heights.size() && y >= 0 && y < heights[0].size() && heights[x][y] >= heights[l][c])
flow(heights, canReach, x, y);
}
}
};提示：关键在于确定起点位置，这道题因为二维数组起点不固定，可以想一想从海上出发，”逆流而上”能到达的点即是可以到达海平面的点。
二、回溯法
算法介绍：回溯法(backtracking)是优先搜索的一种特殊情况，又称为试探法，常用于需要记录节点状态的深度优先搜索。通常来说，排列、组合、选择类问题使用回溯法比较方便。
顾名思义，回溯法的核心是回溯。在搜索到某一节点的时候，如果我们发现目前的节点(及其子节点)并不是需求目标时，我们回退到原来的节点继续搜索，并且把在目前节点修改的状态还原。补充：
- 回溯法修改一般有两种情况，一种是修改最后一位输出，比如排列组合；一种是修改访问标记，比如矩阵里搜字符串。
- 两个小诀窍，一是按引用传状态，二是所有的状态修改在递归完成后回改。
题目一：全排列
给定一个无重复数字的整数数组，求其所有的排列方式。解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> permutedNums;
permute(nums, permutedNums, 0);
return permutedNums;
}
void permute(vector<int>& nums, vector<vector<int>>& permutedNums, int length) {
if (length == nums.size() - 1) {
permutedNums.push_back(nums);
return;
}
for (int i = length; i < nums.size(); ++i) {
swap(nums[i], nums[length]);
permute(nums, permutedNums, length + 1);
swap(nums[i], nums[length]);
}
}
};提示：记得要把swap过的swap回来。
题目二：组合
给定一个整数n和一个整数k，求在1到n中选取k个数字的所有组合方法。解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
vector<vector<int>> combine(int n, int k) {
vector<vector<int>> combinedNums;
vector<int> nums;
combine(combinedNums, nums, n, k, 1);
return combinedNums;
}
void combine(vector<vector<int>>& combinedNums, vector<int>& nums, int n, int k, int length) {
if (nums.size() == k) {
combinedNums.push_back(nums);
return;
}
for (int i = length; i <= n; ++i) {
nums.push_back(i);
combine(combinedNums, nums, n, k, i + 1);
nums.pop_back();
}
}
};提示：和全排列本质上差不多。
题目三：单词搜索
给定一个字母矩阵，所有的字母都与上下左右四个方向上的字母相连。给定一个字符串，求字符串能不能在字母矩阵中寻找到。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
bool exist(vector<vector<char>>& board, string word) {
int m = board.size();
int n = board[0].size();
vector<vector<bool>> visited(m, vector<bool>(n, false));
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (dfs(board, word, 0, i, j, visited)) {
return true;
}
}
}
return false;
}
bool dfs(const vector<vector<char>>& board, const string&word, int length, int x, int y, vector<vector<bool>>&visited) {
if (x < 0 || x >= board.size() || y < 0 || y >= board[0].size() || visited[x][y] || board[x][y] != word[length])
return false;
if (word.length() <= length + 1)
return true;
visited[x][y] = true;
if (dfs(board, word, length + 1, x - 1, y, visited) ||
dfs(board, word, length + 1, x + 1, y, visited) ||
dfs(board, word, length + 1, x, y - 1, visited) ||
dfs(board, word, length + 1, x, y + 1, visited))
return true;
visited[x][y] = false;
return false;
}
};提示：这道题是非常典型的修改访问标记。
题目三：N皇后
按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n皇后问题研究的是如何将n个皇后放置在n×n的棋盘上，并且使皇后彼此之间不能相互攻击。
给你一个整数n，返回所有不同的n皇后问题的解决方案。每一种解法包含一个不同的n皇后问题的棋子放置方案，该方案中’Q’和’.’分别代表了皇后和空位。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution {
public:
vector<vector<string>> solveNQueens(int n) {
vector<vector<string>> res;
vector<string> board(n, string(n, '.'));
vector<pair<int, int>> chess;
for (int i = 0; i < n; ++i)
solve(res, board, n, 0, i, chess);
return res;
}
void solve(vector<vector<string>>& solutions, vector<string>& board, int n, int x, int y, vector<pair<int, int>>& chess) {
if (chess.size() == n - 1) {
board[x][y] = 'Q';
solutions.push_back(board);
board[x][y] = '.';
return;
}
chess.push_back({x, y});
for (int i = 0; i < n; ++i) {
bool flag = false;
for (auto [j, k] : chess) {
if (i == k || abs(x + 1 - j) == abs(i - k)) {
flag = true;
break;
}
}
if (flag) continue;
board[x][y] = 'Q';
solve(solutions, board, n, x + 1, i, chess);
board[x][y] = '.';
}
chess.pop_back();
}
};提示：分析一下状态即可，棋盘的字符即是标志位。
三、广度优先搜索
算法解释：广度优先搜索(breadth-first search，BFS)不同与深度优先搜索，它是一层层进行遍历的，因此需要用先入先出的队列(queue)而非先入后出的栈(stack)进行遍历。由于是按层次进行遍历，广度优先搜索时按照“广”的方向进行遍历的，也常常用来处理最短路径等问题。
1
2
3
4
51
/ \
2 3
/
4考虑上面这棵简单的树，其广度优先搜索的顺序为1->2->3->4。
补充：深度优先搜索和广度优先搜索都可以处理可达性问题，即从一个节点开始是否能达到另一个节点。
题目一：二进制矩阵中的最短路径
给定一个二维0-1矩阵，其中1表示障碍，0表示道路，每个位置与周围八个格子相连。求从左上角到右下角的最短到达距离。如果没有可以到达的方法，返回-1。、
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32class Solution {
private:
vector<int> direction = {-1, -1, 1, 1, -1, 0, 1, 0, -1};
public:
int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
if (grid[0][0] == 1) return -1;
queue<pair<int, int>> location;
int n = grid.size(), depth = 0;
location.push({0, 0});
grid[0][0] = 1;
while (!location.empty()) {
++depth;
int len = location.size();
while (len--) {
auto [i, j] = location.front();
// cout << i << " " << j << endl;
location.pop();
if (i == n - 1 && j == n - 1) return depth;
for (int k = 0; k < 8; ++k) {
int x = i + direction[k];
int y = j + direction[k + 1];
if (x < 0 || x >= n || y < 0 || y >= n || grid[x][y] == 1) continue;
location.push({x, y});
grid[x][y] = 1;
}
}
len = location.size();
}
return -1;
}
};提示：记得改变访问状态。
题目二：最短的桥
给你一个大小为nxn的二元矩阵grid ，其中1表示陆地，0表示水域。岛是由四面相连的1形成的一个最大组，即不会与非组内的任何其他1相连。grid中恰好存在两座岛。
你可以将任意数量的0变为1，以使两座岛连接起来，变成一座岛 。返回必须翻转的0的最小数目。解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47class Solution {
private:
vector<int> direction = {-1, 0, 1, 0, -1};
public:
int shortestBridge(vector<vector<int>>& grid) {
queue<pair<int, int>> location;
int n = grid.size();
int depth = -1;
for (int i = 0; i < n && depth < 0; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) {
findOnePlace(grid, location, i, j, n);
++depth;
break;
}
}
}
while (!location.empty()) {
int length = location.size();
while (length--) {
auto [i, j] = location.front();
location.pop();
for (int k = 0; k < 4; ++k) {
int x = i + direction[k];
int y = j + direction[k + 1];
if (x < 0 || x >= n || y < 0 || y >= n || grid[x][y] == -1) continue;
if (grid[x][y] == 1) return depth;
grid[x][y] = -1;
location.push({x, y});
}
}
length = location.size();
++depth;
}
return -1;
}
void findOnePlace(vector<vector<int>>& grid, queue<pair<int, int>>& location, int x, int y, int n) {
if (x < 0 || x >= n || y < 0 || y >= n || grid[x][y] != 1) return;
location.push({x, y});
grid[x][y] = -1; // record visited location
for (int i = 0; i < 4; ++i) {
findOnePlace(grid, location, x + direction[i], y + direction[i + 1], n);
}
}
};提示：先用深度搜索找到一个岛再找第二个岛。
题目三：单词接龙 II
按字典wordList完成从单词beginWord到单词endWord转化，一个表示此过程的转换序列是形式上像beginWord->s1->s2->…->sk这样的单词序列，并满足：- 每对相邻的单词之间仅有单个字母不同。
- 转换过程中的每个单词si(1<=i<=k)必须是字典wordList中的单词。注意，beginWord不必是字典wordList中的单词。
- s_k == endWord
给你两个单词beginWord和endWord，以及一个字典wordList。请你找出并返回所有从beginWord到endWord的最短转换序列，如果不存在这样的转换序列，返回一个空列表。每个序列都应该以单词列表[beginWord, s1, s2, …, sk]的形式返回。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85class Solution {
public:
vector<vector<string>> findLadders(string beginWord, string endWord, vector<string> &wordList) {
int length = wordList.size();
int wordLength = wordList[0].length();
vector<vector<int>> connection;
vector<string> ladder;
vector<vector<string>> ladders;
vector<bool> visited(length, false);
queue<int> ladderTrace;
vector<int> first;
for (int i = 0; i < length; ++i) {
vector<int> temp;
for (int j = 0; j < length; ++j) {
int count = 0;
for (int k = 0; k < wordLength; ++k) {
if (wordList[i][k] != wordList[j][k])
++count;
}
if (count == 1)
temp.push_back(j);
}
connection.push_back(temp);
}
for (int i = 0; i < length; ++i) {
int count = 0;
for (int j = 0; j < wordLength; ++j) {
if (beginWord[j] != wordList[i][j])
++count;
}
if (count == 1) {
ladderTrace.push(i);
visited[i] = true;
first.push_back(i);
}
}
int depth = 0;
bool flag = false;
while (!ladderTrace.empty() && !flag) {
int count = ladderTrace.size();
++depth;
while (count--) {
int next = ladderTrace.front();
ladderTrace.pop();
if (wordList[next] == endWord) {
flag = true;
break;
}
for (int i : connection[next]) {
if (!visited[i]) {
ladderTrace.push(i);
visited[i] = true;
}
}
}
count = ladderTrace.size();
}
if (depth == 1)
return {{beginWord, endWord}};
ladder.push_back(beginWord);
visited.assign(length, false);
for (int index : first) {
ladder.push_back(wordList[index]);
dfs(wordList, endWord, ladders, ladder, connection, index, visited, depth);
ladder.pop_back();
}
return ladders;
}
void dfs(vector<string>& wordList, string& endWord, vector<vector<string>> &ladders, vector<string> &ladder, vector<vector<int>> &connection, int index, vector<bool> visited, int depth) {
if (depth == 1 && ladder.back() == endWord) {
ladders.push_back(ladder);
return;
}
visited[index] = true;
for (int num : connection[index]) {
if (!visited[num]) {
ladder.push_back(wordList[num]);
dfs(wordList, endWord, ladders, ladder, connection, num, visited, depth - 1);
ladder.pop_back();
}
}
visited[index] = false;
}
};提示：先广度搜索找出最短长度，再用深度搜索找路径，但是我的代码时间超限，还可以继续优化
(我不会了)。
四、练习
题目一：被围绕的区域
给你一个mxn的矩阵board，由若干字符’X’和’O’组成，捕获所有被围绕的区域：- 连接：一个单元格与水平或垂直方向上相邻的单元格连接。
- 区域：连接所有’O’的单元格来形成一个区域。
- 围绕：如果您可以用’X’ 单元格连接这个区域，并且区域中没有任何单元格位于board边缘，则该区域被’X’单元格围绕。
通过原地将输入矩阵中的所有’O’替换为’X’来捕获被围绕的区域。你不需要返回任何值。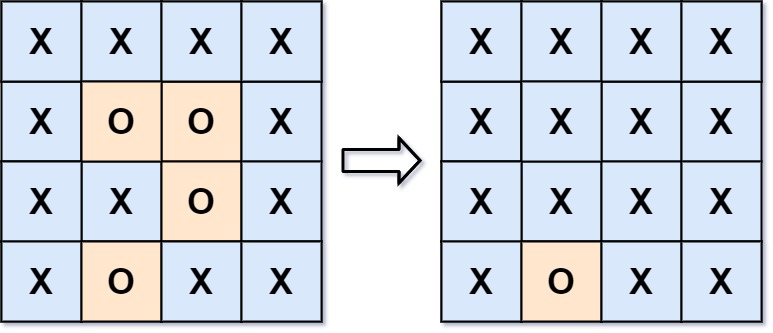
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class Solution {
private:
vector<int> direction = {-1, 0, 1, 0, -1};
public:
void solve(vector<vector<char>>& board) {
int m = board.size();
int n = board[0].size();
for (int i = 0; i < m; ++i) {
if (board[i][0] == 'O') dfs(board, i, 0);
if (board[i][n - 1] == 'O') dfs(board, i, n - 1);
}
for (int j = 0; j < n; ++j) {
if (board[0][j] == 'O') dfs(board, 0, j);
if (board[m - 1][j] == 'O') dfs(board, m - 1, j);
}
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (board[i][j] == '#') board[i][j] = 'O';
else if (board[i][j] == 'O') board[i][j] = 'X';
}
}
}
void dfs(vector<vector<char>>& board, int x, int y) {
board[x][y] = '#';
for (int i = 0; i < 4; ++i) {
int x1 = x + direction[i];
int y1 = y + direction[i + 1];
if (x1 < 0 || x1 >= board.size() || y1 < 0 || y1 >= board[0].size()) continue;
if (board[x1][y1] == 'O') dfs(board, x1, y1);
}
}
};提示：和大西洋太平洋水流问题差不多，因为起点如果从’X’开始，那么会很麻烦，不如从边缘的’O’开始。
题目二：组合总和 II
给定一个候选人编号的集合candidates和一个目标数target，找出candidates中所有可以使数字和为target的组合。
candidates中的每个数字在每个组合中只能使用一次，解集不能包含重复的组合。解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29class Solution {
public:
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
sort(candidates.begin(), candidates.end());
vector<vector<int>> res;
vector<int> temp;
vector<bool> onPath(candidates.size(), false);
dfs(res, temp, onPath, candidates, 0, 0, target);
return res;
}
void dfs(vector<vector<int>>& res, vector<int>& candidate, vector<bool>& onPath, const vector<int>& candidates, int depth, int sum, const int target) {
if (sum > target) return;
if (sum == target) {
res.push_back(candidate);
return;
}
for (int i = depth; i < candidates.size(); ++i) {
candidate.push_back(candidates[i]);
onPath[i] = true;
sum += candidates[i];
if (i == 0 || candidates[i] != candidates[i - 1] || (candidates[i] == candidates[i - 1] && onPath[i - 1]))
dfs(res, candidate, onPath, candidates, i + 1, sum, target);
candidate.pop_back();
onPath[i] = false;
sum -= candidates[i];
}
}
};提示：主要是需要记录相同的值的出现情况。做完这道题也可以尝试全排列 II
题目三：解数独
编写一个程序，通过填充空格来解决数独问题。
数独的解法需遵循如下规则：- 数字1-9在每一行只能出现一次。
- 数字1-9在每一列只能出现一次。
- 数字1-9在每一个以粗实线分隔的3x3宫内只能出现一次。（请参考示例图）
数独部分空格内已填入了数字，空白格用’.’表示。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43class Solution {
private:
vector<vector<bool>> hash1;
vector<vector<bool>> hash2;
vector<vector<bool>> hash3;
bool valid;
public:
Solution() : hash1(9, vector<bool>(9, false)), hash2(9, vector<bool>(9, false)), hash3(9, vector<bool>(9, false)), valid(false) {}
void solveSudoku(vector<vector<char>>& board) {
vector<pair<int, int>> locations;
for (int i = 0; i < 9; ++i) {
for (int j = 0; j < 9; ++j) {
if (board[i][j] == '.') {
locations.push_back({i, j});
continue;
}
hash1[i][board[i][j] - '0' - 1] = true;
hash2[j][board[i][j] - '0' - 1] = true;
hash3[(i / 3) * 3 + j / 3][board[i][j] - '0' - 1] = true;
}
}
int size = locations.size();
dfs(board, locations, 0, size);
}
void dfs(vector<vector<char>>& board, const vector<pair<int, int>>& locations, int depth, const int size) {
if (depth == size) {
valid = true;
return;
}
auto [i, j] = locations[depth];
for (int k = 1; k < 10 && !valid; ++k) {
if (!hash1[i][k - 1] && !hash2[j][k - 1] && !hash3[(i / 3) * 3 + j / 3][k - 1]) {
hash1[i][k - 1] = hash2[j][k - 1] = hash3[(i / 3) * 3 + j / 3][k - 1] = true;
board[i][j] = k + '0';
dfs(board, locations, depth + 1, size);
hash1[i][k - 1] = hash2[j][k - 1] = hash3[(i / 3) * 3 + j / 3][k - 1] = false;
}
}
}
};提示：暴力的深度搜索即可，记得记录状态。
题目四：最小深度树
树是一个无向图，其中任何两个顶点只通过一条路径连接。换句话说，任何一个没有简单环路的连通图都是一棵树。
给你一棵包含n个节点的树，标记为0到n-1。给定数字n和一个有n-1条无向边的edges列表(每一个边都是一对标签)，其中edges[i]=[ai, bi]表示树中节点ai和bi之间存在一条无向边。可选择树中任何一个节点作为根。当选择节点x作为根节点时，设结果树的高度为h。在所有可能的树中，具有最小高度的树(即，min(h))被称为最小高度树 。
请你找到所有的最小高度树并按任意顺序返回它们的根节点标签列表。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43class Solution {
public:
vector<int> findMinHeightTrees(int n, vector<vector<int>> &edges) {
if (n <= 2) {
vector<int> res;
for (int i = 0; i < n; ++i) {
res.push_back(i);
}
return res;
}
vector<vector<int>> adj(n);
vector<int> degree(n, 0);
for (const auto &edge : edges) {
adj[edge[0]].push_back(edge[1]);
adj[edge[1]].push_back(edge[0]);
degree[edge[0]]++;
degree[edge[1]]++;
}
queue<int> q;
for (int i = 0; i < n; ++i) {
if (degree[i] == 1) q.push(i);
}
int remainingNodes = n;
while (remainingNodes > 2) {
int levelSize = q.size();
remainingNodes -= levelSize;
for (int i = 0; i < levelSize; ++i) {
int u = q.front();
q.pop();
for (int v : adj[u]) {
degree[v]--;
if (degree[v] == 1) q.push(v);
}
}
}
vector<int> res;
while (!q.empty()) {
res.push_back(q.front());
q.pop();
}
return res;
}
};提示：需要用到图论的知识——拓扑排序。
相关推荐
2025-08-25
LeetCode刷题笔记(一): 贪心
贪心算法的核心思想：局部最优以实现全局最优。 一、分配问题 题目：分发糖果n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。你需要按照以下要求，给这些孩子分发糖果： 每个孩子至少分配到 1 个糖果。 相邻两个孩子中，评分更高的那个会获得更多的糖果。请你给每个孩子分发糖果，计算并返回需要准备的最少糖果数目。 解答： 123456789101112131415161718class Solution {public: int candy(vector<int> &ratings) { int n = ratings.size(); vector<int> candies(n, 1); for (int i = 1; i < n; ++i) { if (ratings[i] > ratings[i - 1]) { candies[i] = candies[i - 1] +...
2025-09-21
LeetCode刷题笔记(九): 位运算
常用技巧(其中0s和1s分别表示只由0或1构成的二进制数字。)：123x ^ 0s = x x & 0s = 0 x | 0s = xx ^ 1s = ~x x & 1s = x x | 1s = 1sx ^ x = 0 x & x = x x | x = x 除此之外，n&(n-1)可以去除n的位级表示中最低的那一位，例如对于二进制表示11110100，减去1得到11110011，这两个数按位与得到11110000。n&(-n)可以得到n的位级表示中最低的那一位，例如对于二进制表示11110100，取负得到00001100，这两个数按位与得到00000100。 一、位运算基础问题 题目一：汉明距离给定两个十进制数字，求它们二进制表示的汉明距离(Hamming distance，即不同位的个数)。 解答： 12345678910111213class Solution {public: int hammingDistance(int x, int y)...
2025-08-26
LeetCode刷题笔记(二): 双指针
双指针算法的核心思想：双指针主要用于遍历数组，两个指针指向不同的元素，从而协同完成任务。也可以延伸到多个数组的多个指针。 一、Two Sum 题目：两数之和 II - 输入有序数组给你一个下标从1开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。 解答： 12345678910vector<int> twoSum(vector<int>& numbers, int target) { int l = 0, r = numbers.size() - 1, two_sum; while (l < r) { ...
2025-08-27
LeetCode刷题笔记(三): 二分查找
二分查找算法的核心思想：二分查找也常被称为二分法或者折半查找 (binary search, bisect)，每次查找时通过将待查找的单调区间分成两部分并只取一部分继续查找，将查找的复杂度大大减少。对于一个长度为O(n)的数组，二分查找的时间复杂度为O(logn)。 一、求开方 题目：x 的平方根给定一个非负整数 x，求它的开方，向下取整。 解答： 12345678910111213141516int mySqrt(int x) { int l = 1, r = x, mid, x_div_mid; while (l <= r) { mid = l + (r - l) / 2; x_div_mid = x / mid; if (mid == x_div_mid) { return mid; } if (mid < x_div_mid) { l = mid + 1; }...
2025-09-15
LeetCode刷题笔记(七): 数学问题
一、最大公约数和最小公倍数这个没什么好说的，辗转相除法： 1234567int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }int lcm(int a, int b) { return a * b / gcd(a, b); } 也可以通过扩展欧几里得算法(extended gcd)在求得a和b最大公因数的同时，也得到它们的系数x和y，从而使ax+by=gcd(a, b)，也就是贝祖等式。 12345678910int xGCD(int a, int b, int &x, int &y) { if (b == 0) { x = 1, y = 0; return a; } int x_inner, y_inner; int gcd = xGCD(b, a % b, x_inner, y_inner); x = y_inner, y =...
2025-08-28
LeetCode刷题笔记(四): 排序
排序算法：包括快排，归并排序，桶排序，哈希排序等。 一、快排 算法介绍：对于当前一个未排序片段，我们先随机选择一个位置当作中枢点，然后通过遍历操作，将所有比中枢点小的数字移动到其左侧，再将所有比中枢点大的数字移动到其右侧。操作完成后，我们再次对中枢点左右侧的片段再次进行快速排序即可。可证明，如果中枢点选取是随机的，那么该算法的平均复杂度可以达到O(nlogn)，最差情况下复杂度则为O(n^2)。 代码： 1234567891011121314151617void quickSort(vector<int> &nums, int l, int r) { if (l >= r) return; int pivot = l + (rand() % (r - l + 1)); int pivot_val = nums[pivot]; swap(nums[l], nums[pivot]); int i = l + 1, j = r; while (true) { while (i < j &&...
评论
