LeetCode刷题笔记(十三): 树
算法介绍：作为(单)链表的升级版，我们通常接触的树都是二叉树(binary tree)，即每个节点最多有两个子节点；且除非题目说明，默认树中不存在循环结构。
- 代码实现：
1
2
3
4
5
6struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
一、树的递归
题目一：二叉树的最大深度
求一个二叉树的最大深度。
解答：
1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
int maxDepth(TreeNode* root) {
if (root == nullptr) return 0;
int depth = 0;
if (root->left != nullptr)
depth = maxDepth(root->left);
if (root->right != nullptr)
depth = max(maxDepth(root->right), depth);
return 1 + depth;
}
};提示：很简单，非常基础。
题目二：平衡二叉树
判断一个二叉树是否平衡。树平衡的定义是，对于树上的任意节点，其两侧节点的最大深度的差值不得大于1。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
private:
int maxDepth(TreeNode *root) {
if (root == nullptr) return 0;
return max(maxDepth(root->left), maxDepth(root->right)) + 1;
}
public:
bool isBalanced(TreeNode* root) {
if (root == nullptr) return true;
int left = maxDepth(root->left);
int right = maxDepth(root->right);
if (abs(left - right) > 1) return false;
else return isBalanced(root->left) && isBalanced(root->right);
}
};提示：很简单，利用之前的深度计算方法来比较一下就行了。
题目三：二叉树的直径
求一个二叉树的最长直径。直径的定义是二叉树上任意两节点之间的无向距离。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
private:
int updateDiameter(TreeNode *node, int &diameter) {
if (node == nullptr) return 0;
int left = updateDiameter(node->left, diameter);
int right = updateDiameter(node->right, diameter);
diameter = max(diameter, left + right);
return max(left, right) + 1;
}
public:
int diameterOfBinaryTree(TreeNode *root) {
int diameter = 0;
updateDiameter(root, diameter);
return diameter;
}
};提示：最大直径就是左边最大深度+右边最大深度。
题目四：路径总和 III
给定一个整数二叉树，求有多少条路径节点值的和等于给定值。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution {
private:
void calculatePath(TreeNode* root, long long targetSum, int& sum) {
if (root == nullptr) return;
if (targetSum == root->val) ++sum;
calculatePath(root->left, targetSum - root->val, sum);
calculatePath(root->right, targetSum - root->val, sum);
}
public:
int pathSum(TreeNode* root, int targetSum) {
if (root == nullptr) return 0;
int sum = 0;
queue<TreeNode *> tree;
tree.push(root);
while (!tree.empty()) {
int size = tree.size();
while (size--) {
TreeNode *node = tree.front();
tree.pop();
calculatePath(node, (long long) targetSum, sum);
if (node->left != nullptr)
tree.push(node->left);
if (node->right != nullptr)
tree.push(node->right);
}
}
return sum;
}
};提示：需要遍历每个节点作为起点，然后往下遍历所有路径。
题目五：对称二叉树
判断一个二叉树是否对称。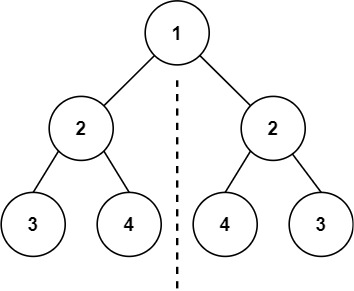
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
private:
bool isLeftRightSymmetric(TreeNode* left, TreeNode* right) {
if (left == nullptr && right == nullptr)
return true;
if (left == nullptr || right == nullptr)
return false;
if (left->val != right->val)
return false;
return isLeftRightSymmetric(left->left, right->right) && isLeftRightSymmetric(left->right, right->left);
}
public:
bool isSymmetric(TreeNode* root) {
if (root == nullptr) return true;
return isLeftRightSymmetric(root->left, root->right);
}
};提示：主要是要注意遍历顺序，左左对右右，左右对右左。
题目六：删点成林
给定一个整数二叉树和一些整数，求删掉这些整数对应的节点后，剩余的子树。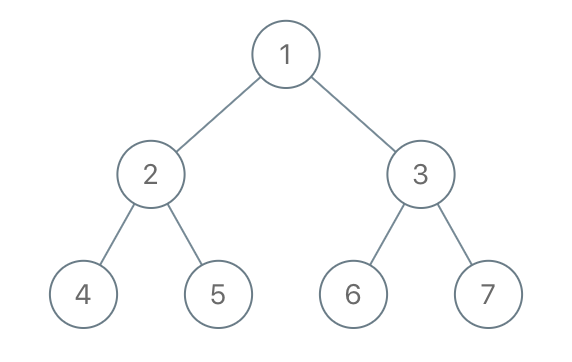
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
private:
TreeNode *dfs(TreeNode *node, const unordered_set<int> &to_delete, vector<TreeNode *> &res) {
if (!node) return nullptr;
node->left = dfs(node->left, to_delete, res);
node->right = dfs(node->right, to_delete, res);
if (to_delete.count(node->val)) {
if (node->left)
res.push_back(node->left);
if (node->right)
res.push_back(node->right);
return nullptr;
}
return node;
}
public:
vector<TreeNode *> delNodes(TreeNode *root, vector<int> &to_delete) {
unordered_set<int> delete_set(to_delete.begin(), to_delete.end());
vector<TreeNode *> res;
TreeNode *newRoot = dfs(root, delete_set, res);
if (newRoot) res.push_back(newRoot);
return res;
}
};提示：这道题的重点是通过递归去寻找出正确的左节点或者是右节点。
二、层次遍历
题目：二叉树的层平均值
给定一个二叉树，求每一层的节点值的平均数。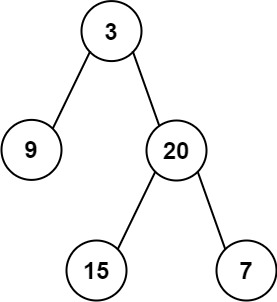
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
vector<double> averageOfLevels(TreeNode* root) {
vector<double> res;
queue<TreeNode *> q;
q.push(root);
while (!q.empty()) {
double sum = 0, count = 0;
int size = q.size();
while (size--) {
TreeNode *node = q.front();
q.pop();
sum += node->val;
++count;
if (node->left != nullptr)
q.push(node->left);
if (node->right != nullptr)
q.push(node->right);
}
res.push_back(sum / count);
}
return res;
}
};提示：很简单的广度优先搜索。
三、前中后序遍历
算法解释：前序遍历、中序遍历和后序遍历是三种利用深度优先搜索遍历二叉树的方式。它们是在对节点访问的顺序有一点不同，其它完全相同。考虑如下一棵树：
1
2
3
4
51
/ \
2 3
/ \ \
4 5 6- 前序遍历为：1->2->4->5->3->6
- 中序遍历为：4->2->5->1->3->6
- 后序遍历为：4->5->2->6->3->1
题目一：从前序与中序遍历序列构造二叉树
给定一个二叉树的前序遍历和中序遍历结果，尝试复原这个树。已知树里不存在重复值的节点。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
private:
TreeNode *createTree(const vector<int> &preorder, const unordered_map<int, int> &inMap, int inLeft, int inRight, int &preIndex) {
if (inLeft > inRight) return nullptr;
int rootVal = preorder[preIndex++];
TreeNode *root = new TreeNode(rootVal);
int mid = inMap.at(rootVal);
root->left = createTree(preorder, inMap, inLeft, mid - 1, preIndex);
root->right = createTree(preorder, inMap, mid + 1, inRight, preIndex);
return root;
}
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
unordered_map<int, int> inorderMap;
int size = preorder.size();
for (int i = 0; i < size; ++i)
inorderMap[inorder[i]] = i;
int preIndex = 0;
return createTree(preorder, inorderMap, 0, size - 1, preIndex);
}
};提示：非常经典的构造树的方法，主要是要去递归地划分左子树和右子树，而这个必须要依靠中序遍历来完成，这也就是为什么没有中序遍历无法确定一棵树的原因。
题目二：二叉树的前序遍历
实现二叉树的前序遍历。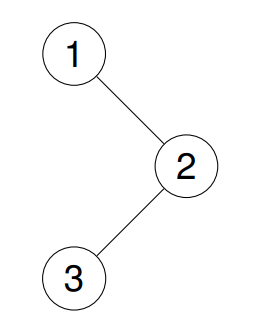
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
private:
void preorder(TreeNode* root, vector<int>& res) {
res.push_back(root->val);
if (root->left != nullptr)
preorder(root->left, res);
if (root->right != nullptr)
preorder(root->right, res);
}
public:
vector<int> preorderTraversal(TreeNode* root) {
if (root == nullptr) return {};
vector<int> res;
preorder(root, res);
return res;
}
};提示：不是用递归的话需要使用栈来实现，本质上其实是一样的。
四、二叉搜索树
算法解释：二叉查找树(Binary Search Tree, BST)是一种特殊的二叉树：对于每个父节点，其左子树中所有节点的值小于等于父结点的值，其右子树中所有节点的值大于等于父结点的值。因此对于一个二叉查找树，我们可以在O(log n)的时间内查找一个值是否存在：从根节点开始，若当前节点的值大于查找值则向左下走，若当前节点的值小于查找值则向右下走。同时因为二叉查找树是有序的，对其中序遍历的结果即为排好序的数组。
例如下图：
1
2
3
4
54
/ \
2 5
/ \ \
1 3 6其中序遍历结果为：1->2->3->4->5->6。
题目一：恢复二叉搜索树
给定一个二叉查找树，已知有两个节点被不小心交换了，试复原此树。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
private:
void findMistakes(TreeNode* root, TreeNode* &mistake1, TreeNode* &mistake2, TreeNode* &prev) {
if (root == nullptr) return;
findMistakes(root->left, mistake1, mistake2, prev);
if (prev != nullptr && prev->val > root->val) {
if (mistake1 == nullptr) mistake1 = prev;
mistake2 = root;
}
prev = root;
findMistakes(root->right, mistake1, mistake2, prev);
}
public:
void recoverTree(TreeNode* root) {
TreeNode *mistake1 = nullptr, *mistake2 = nullptr;
TreeNode *prev = nullptr;
findMistakes(root, mistake1, mistake2, prev);
swap(mistake1->val, mistake2->val);
}
};提示：注意使用中序遍历来对节点进行比较，因为中序遍历前节点一定小于后节点。
题目二：修剪二叉搜索树
给定一个二叉查找树和两个整数L和R，且L<R，试修剪此二叉查找树，使得修剪后所有节点的值都在[L, R]的范围内。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (root == nullptr) return nullptr;
if (root->val < low)
return trimBST(root->right, low, high);
if (root->val > high)
return trimBST(root->left, low, high);
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
return root;
}
};提示：没啥好说的，学会利用搜索树的性质：大于就返回左边更小的子树，小于就返回右边更大的子树。
五、字典树
算法解释：字典树(Trie)用于判断字符串是否存在或者是否具有某种字符串前缀。假如我们有一个储存了近万个单词的字典，即使我们使用哈希，在其中搜索一个单词的实际开销也是非常大的，且无法轻易支持搜索单词前缀。然而由于一个英文单词的长度n通常在10以内，如果我们使用字典树，则可以在O(n)——近似 O(1)的时间内完成搜索，且额外开销非常小。
题目：实现 Trie (前缀树)
尝试建立一个字典树，支持快速插入单词、查找单词、查找单词前缀的功能。解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57struct TrieTree {
bool is_end;
vector<TrieTree*> children;
TrieTree() : is_end(false), children(26, nullptr) {}
};
class Trie {
public:
Trie() {
root = new TrieTree();
}
~Trie() {
deleteNode(root);
}
void insert(string word) {
TrieTree* node = root;
for (char c : word) {
int idx = c - 'a';
if (node->children[idx] == nullptr)
node->children[idx] = new TrieTree();
node = node->children[idx];
}
node->is_end = true;
}
bool search(string word) {
TrieTree *node = root;
for (char c : word) {
if (node == nullptr) break;
int idx = c - 'a';
node = node->children[idx];
}
return node != nullptr && node->is_end;
}
bool startsWith(string prefix) {
TrieTree *node = root;
for (char c : prefix) {
if (node == nullptr) break;
int idx = c - 'a';
node = node->children[idx];
}
return node != nullptr;
}
private:
TrieTree* root;
void deleteNode(TrieTree* node) {
if (!node) return;
for (TrieTree* child : node->children) {
deleteNode(child);
}
delete node;
}
};提示：实现起来并不是很困难，用一个bool变量更便捷的判断是否为一个单词的末尾，注意一下边界条件。
六、练习
题目一：翻转二叉树
给你一棵二叉树的根节点root，翻转这棵二叉树，并返回其根节点。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
private:
void invert(TreeNode* root) {
if (root == nullptr) return;
TreeNode *temp = root->left;
root->left = root->right;
root->right = temp;
invert(root->left);
invert(root->right);
}
public:
TreeNode* invertTree(TreeNode* root) {
invert(root);
return root;
}
};提示：还是比较简单的，递归的处理一下就行了。
题目二：合并二叉树
给你两棵二叉树：root1和root2。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为null的节点将直接作为新二叉树的节点。返回合并后的二叉树。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if (root1 == nullptr && root2 == nullptr)
return nullptr;
if (root1 == nullptr && root2 != nullptr)
return root2;
if (root1 != nullptr && root2 == nullptr)
return root1;
root1->left = mergeTrees(root1->left, root2->left);
root1->right = mergeTrees(root1->right, root2->right);
root1->val += root2->val;
return root1;
}
};提示：不难，处理完为nullptr的情况后剩余的节点直接相加即可。
题目三：另一棵树的子树
给你两棵二叉树root和subRoot。检验root中是否包含和subRoot具有相同结构和节点值的子树。如果存在，返回true；否则，返回false。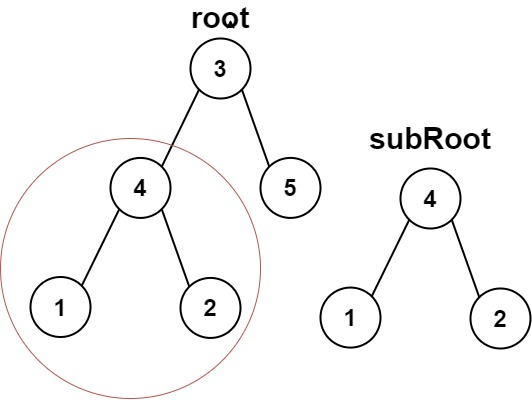
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
private:
bool isSametree(TreeNode* root1, TreeNode* root2) {
if (root1 == nullptr && root2 == nullptr)
return true;
if (root1 == nullptr || root2 == nullptr)
return false;
if (root1->val != root2->val)
return false;
return isSametree(root1->left, root2->left) && isSametree(root1->right, root2->right);
}
public:
bool isSubtree(TreeNode* root, TreeNode* subRoot) {
if (root == nullptr) return false;
return isSametree(root, subRoot) || isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}
};提示：subTree肯定需要遍历一遍root的节点，所以对每个根节点进行是否是同样的树的判断即可。
题目四：左叶子之和
给定二叉树的根节点 root ，返回所有左叶子之和。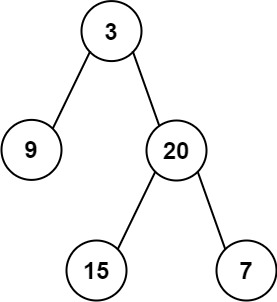
解答：
1
2
3
4
5
6
7
8class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if (root == nullptr) return 0;
return (root->left != nullptr && root->left->left == nullptr && root->left->right == nullptr ? root->left->val : 0)
+ sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);
}
};提示：重点是要加上所有的左叶子节点，每次遍历到一个点之后判断其左节点是不是叶子节点即可。
题目五：找树左下角的值
给定一个二叉树的根节点root，请找出该二叉树的最底层最左边节点的值。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
queue<TreeNode *> nodes;
nodes.push(root);
int firstOfEachLayer = 0;
while (!nodes.empty()) {
int size = nodes.size();
firstOfEachLayer = nodes.front()->val;
while (size--) {
TreeNode *temp = nodes.front();
nodes.pop();
if (temp->left != nullptr)
nodes.push(temp->left);
if (temp->right != nullptr)
nodes.push(temp->right);
}
}
return firstOfEachLayer;
}
};提示：简单的广搜即可，不知道为什么是中等题，使用递归的话比较麻烦，时间复杂度也偏高。
题目六：把二叉搜索树转换为累加树
给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树(Greater Sum Tree)，使每个节点node的新值等于原树中大于或等于node.val的值之和。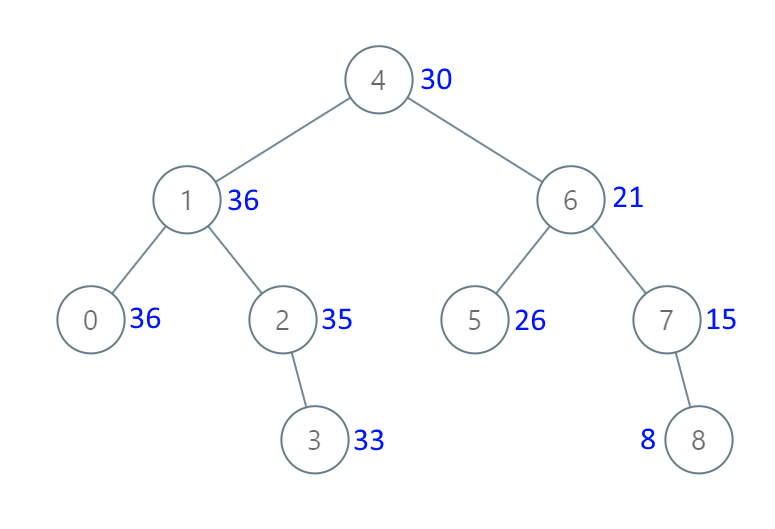
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
private:
int transferToBST(TreeNode* &root, int num) {
if (root == nullptr) return num;
root->val += transferToBST(root->right, num);
int rightTreeSum = (root->left != nullptr ? transferToBST(root->left, root->val) : root->val);
return rightTreeSum;
}
public:
TreeNode* convertBST(TreeNode* root) {
transferToBST(root, 0);
return root;
}
};提示：重点在于左节点如何获取到右节点的累加值，不能简单地直接往右节点递归，因为左节点的右子节点也要继承左节点的父结点的值。
题目七：二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先，一个节点也可以是它自己的祖先。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
private:
TreeNode* findAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root->val > q->val)
return findAncestor(root->left, p, q);
if (root->val < p->val)
return findAncestor(root->right, p, q);
return root;
}
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (p->val > q->val) {
TreeNode* tmp = p;
p = q;
q = tmp;
}
return findAncestor(root, p, q);
}
};提示：没啥难的，利用搜索树的性质，两个都小于当前节点那么必然都在当前节点的左边，反之则在右边。
题目八：二叉搜索树的最小绝对差
给你一个二叉搜索树的根节点root，返回树中任意两不同节点值之间的最小的差值绝对值。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
private:
void inorder(TreeNode* node, int& prevVal, bool& hasPrev, int& minNum) {
if (!node) return;
inorder(node->left, prevVal, hasPrev, minNum);
if (hasPrev) minNum = min(minNum, node->val - prevVal);
else hasPrev = true;
prevVal = node->val;
inorder(node->right, prevVal, hasPrev, minNum);
}
public:
int getMinimumDifference(TreeNode* root) {
int minNum = 100001;
int prevVal = 0;
bool hasPrev = false;
inorder(root, prevVal, hasPrev, minNum);
return minNum;
}
};提示：同样利用中序遍历来完成，这种遍历方法可以记一下，同样需要利用中序遍历的有恢复二叉搜索树。
题目九：好叶子节点对的数量
如果二叉树中两个叶节点之间的最短路径长度小于或者等于distance，那它们就可以构成一组好叶子节点对。返回树中好叶子节点对的数量。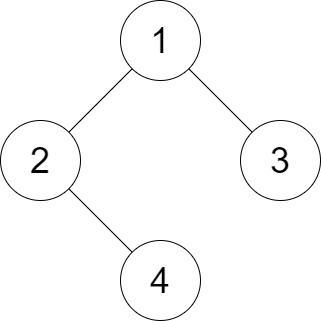
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29class Solution {
private:
vector<int> calculate(TreeNode* root, const int& distance, int& count) {
if (root == nullptr) return vector<int>();
if (root->left == nullptr && root->right == nullptr)
return vector<int>(1, 1);
auto leftDistances = calculate(root->left, distance, count);
auto rightDistances = calculate(root->right, distance, count);
for (int leftDistance : leftDistances) {
for (int rightDistance : rightDistances) {
if (leftDistance + rightDistance <= distance)
++count;
}
}
vector<int> res;
for (int d : leftDistances)
if (d + 1 <= distance) res.push_back(d + 1);
for (int d : rightDistances)
if (d + 1 <= distance) res.push_back(d + 1);
return res;
}
public:
int countPairs(TreeNode* root, int distance) {
int count = 0;
calculate(root, distance, count);
return count;
}
};提示：因为要记录所有叶结点的距离，所以需要返回
vector<int>，其余部分和二叉树的直径类似。题目十：根据前序和后序遍历构造二叉树
给定一个二叉树的前序遍历和后序遍历结果，尝试复原这个树(答案不唯一)。已知树里不存在重复值的节点。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
private:
TreeNode* createTree(const vector<int>& preorder, const unordered_map<int, int>& postMap, int l, int r, int& preIdx) {
if (r - l < 1) {
if (r - l < 0) return nullptr;
return new TreeNode(preorder[preIdx++]);
}
TreeNode *root = new TreeNode(preorder[preIdx++]);
int mid = postMap.at(preorder[preIdx]);
root->left = createTree(preorder, postMap, l, mid, preIdx);
root->right = createTree(preorder, postMap, mid + 1, r - 1, preIdx);
return root;
}
public:
TreeNode* constructFromPrePost(vector<int>& preorder, vector<int>& postorder) {
int size = preorder.size(), preIdx = 0;
unordered_map<int, int> postMap;
for (int i = 0; i < size; ++i)
postMap[postorder[i]] = i;
return createTree(preorder, postMap, 0, size - 1, preIdx);
}
};提示：因为后序遍历无法通过当前根节点划分左右子树，所以需要去通过当前节点的子节点来划分，这样做的话为了避免越界需要让递归提前结束。
题目十一：从中序与后序遍历序列构造二叉树
给定一个二叉树的后序遍历和后序遍历结果，尝试复原这个树。已知树里不存在重复值的节点。解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
private:
TreeNode* createTree(const vector<int>& postorder, const unordered_map<int, int>& inMap, int l, int r, int& postIdx) {
if (l > r) return nullptr;
int rootVal = postorder[postIdx--];
TreeNode *root = new TreeNode(rootVal);
int mid = inMap.at(rootVal);
root->right = createTree(postorder, inMap, mid + 1, r, postIdx);
root->left = createTree(postorder, inMap, l, mid - 1, postIdx);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int size = postorder.size(), postIdx = size - 1;
unordered_map<int, int> inMap;
for (int i = 0; i < size; ++i)
inMap[inorder[i]] = i;
return createTree(postorder, inMap, 0, size - 1, postIdx);
}
};提示：与从前序与中序遍历序列构造二叉树的遍历方向相反即可。
题目十二：二叉树的中序遍历
实现二叉树的中序遍历。解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
if (root == nullptr) return {};
vector<int> res;
stack<TreeNode *> stack;
stack.push(root);
while (!stack.empty()) {
TreeNode *node = stack.top();
if (node->left != nullptr) {
stack.push(node->left);
node->left = nullptr;
continue;
}
stack.pop();
res.push_back(node->val);
if (node->right != nullptr) {
stack.push(node->right);
node->right = nullptr;
}
}
return res;
}
};提示：这是非递归的写法，使用了栈，递归写法非常简单不展示了。
题目十三：二叉树的后序遍历
实现二叉树的后序遍历。解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33class Solution {
// private:
// void postorderTraversalByRecursion(TreeNode* root, vector<int>& res) {
// if (root == nullptr) return;
// postorderTraversalByRecursion(root->left, res);
// postorderTraversalByRecursion(root->right, res);
// res.push_back(root->val);
// }
public:
vector<int> postorderTraversal(TreeNode* root) {
if (root == nullptr) return {};
vector<int> res;
stack<TreeNode *> stack;
stack.push(root);
while (!stack.empty()) {
TreeNode *node = stack.top();
if (node->left != nullptr) {
stack.push(node->left);
node->left = nullptr;
continue;
}
if (node->right != nullptr) {
stack.push(node->right);
node->right = nullptr;
continue;
}
stack.pop();
res.push_back(node->val);
}
return res;
}
};提示：两种写法都展示出来了。
题目十四：二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
解答：
1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q) {
if (root == nullptr || root == p || root == q)
return root;
TreeNode *left = lowestCommonAncestor(root->left, p, q);
TreeNode *right = lowestCommonAncestor(root->right, p, q);
if (left == nullptr) return right;
if (right == nullptr) return left;
return root;
}
};提示：仍然是使用递归，相对于二叉搜索树的最近公共祖先这道题的判断不再是节点的大小关系而是是否都在左边或者是右边(通过nullptr来判断)，如果不都在同一边则当前节点为祖先。
题目十五：两数之和 IV - 输入二叉搜索树
给定一个二叉搜索树root和一个目标结果k，如果二叉搜索树中存在两个元素且它们的和等于给定的目标结果，则返回true。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
private:
void inorderTraversal(TreeNode* root, vector<int>& nums) {
if (root == nullptr) return;
inorderTraversal(root->left, nums);
nums.push_back(root->val);
inorderTraversal(root->right, nums);
}
public:
bool findTarget(TreeNode* root, int k) {
vector<int> nums;
inorderTraversal(root, nums);
int start = 0, end = nums.size() - 1;
while (start < end) {
if (k - nums[start] == nums[end])
return true;
if (k - nums[start] > nums[end])
++start;
else --end;
}
return false;
}
};提示：很简单，别想着使用空间复杂度为O(1)的解法了。
题目十六：删除二叉搜索树中的节点
给定一个二叉搜索树的根节点root和一个值key，删除二叉搜索树中的key对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42class Solution {
private:
TreeNode* findNode(TreeNode* root, TreeNode* &prev, const int key) {
if (root == nullptr) return nullptr;
if (root->val == key) return root;
prev = root;
if (root->val < key)
return findNode(root->right, prev, key);
return findNode(root->left, prev, key);
}
public:
TreeNode* deleteNode(TreeNode* root, int key) {
TreeNode *dummy = new TreeNode(100001);
dummy->left = root;
TreeNode *toDeletePrev = dummy;
TreeNode *toDelete = findNode(root, toDeletePrev, key);
if (toDelete == nullptr) return dummy->left;
bool flag = toDeletePrev->val > toDelete->val;
TreeNode *toReplacePrev = nullptr;
TreeNode *toReplace = toDelete->right;
if (toReplace == nullptr) {
if (flag) toDeletePrev->left = toDelete->left;
else toDeletePrev->right = toDelete->left;
delete toDelete;
return dummy->left;
}
while (toReplace->left != nullptr) {
toReplacePrev = toReplace;
toReplace = toReplace->left;
}
if (toReplacePrev)
toReplacePrev->left = toReplace->right;
else toDelete->right = toReplace->right;
toReplace->left = toDelete->left;
toReplace->right = toDelete->right;
if (flag) toDeletePrev->left = toReplace;
else toDeletePrev->right = toReplace;
delete toDelete;
return dummy->left;
}
};提示：实际上并不难，想好替换的步骤即可，对于替换的节点有两种选择：左子树的最右节点或者是右子树的最左节点。
题目十七：有序链表转换二叉搜索树
给定一个单链表的头节点head，其中的元素按升序排序，将其转换为平衡二叉搜索树。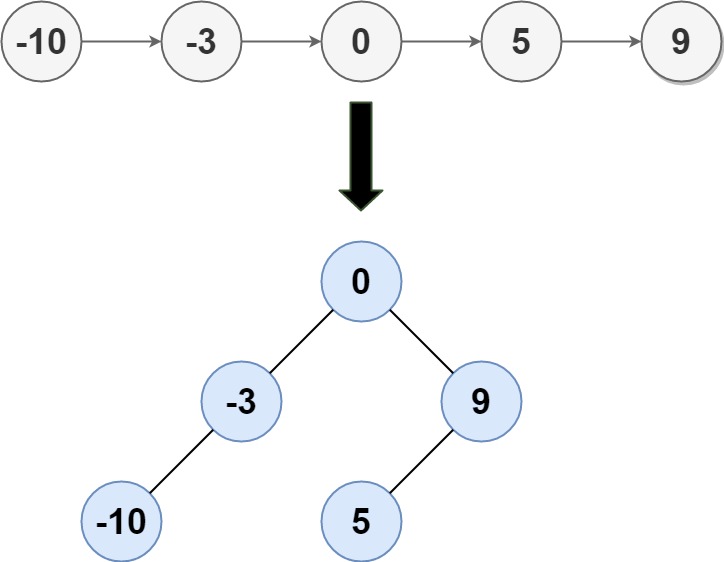
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
private:
TreeNode* buildTreeByList(ListNode* head, int l, int r) {
if (l > r) return nullptr;
ListNode *mid = head;
int steps = (r - l) >> 1;
for (int i = 0; i < steps; ++i)
mid = mid->next;
TreeNode *node = new TreeNode(mid->val);
ListNode *right = mid->next;
mid = nullptr;
node->left = buildTreeByList(head, l, l + steps - 1);
node->right = buildTreeByList(right, l + steps + 1, r);
return node;
}
public:
TreeNode* sortedListToBST(ListNode* head) {
ListNode *temp = head;
int size = 0;
while (temp != nullptr) {
++size;
temp = temp->next;
}
return buildTreeByList(head, 0, size - 1);
}
};提示：还是比较简单的，主要思路是先找到中间节点然后进行两边的分治，因为是平衡二叉树所以每次找中间节点当作树的根节点即可。
题目十八：递增顺序搜索树
给你一棵二叉搜索树的root，请你按中序遍历将其重新排列为一棵递增顺序搜索树。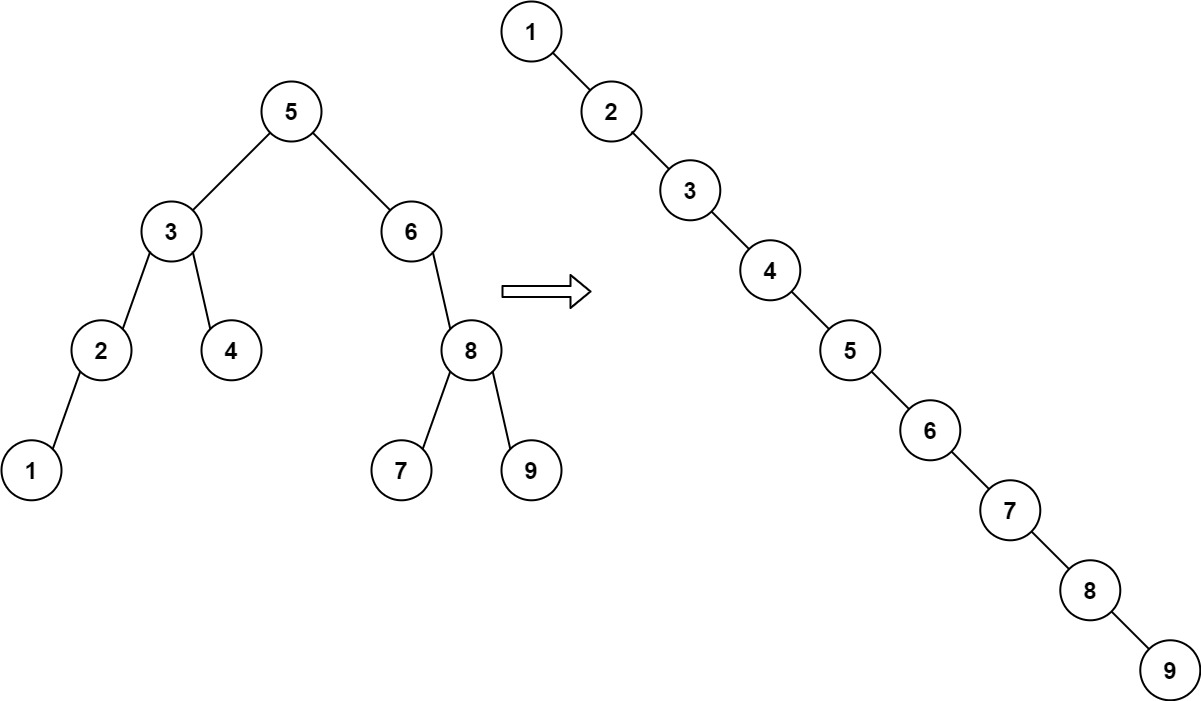
解答：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
TreeNode* increasingBST(TreeNode* root) {
TreeNode *dummy = new TreeNode();
TreeNode *opTree = dummy;
stack<TreeNode *> s;
s.push(root);
while (!s.empty()) {
TreeNode *node = s.top();
if (node->left != nullptr) {
s.push(node->left);
node->left = nullptr;
continue;
}
opTree->right = new TreeNode(node->val);
opTree = opTree->right;
s.pop();
if (node->right != nullptr) {
s.push(node->right);
node->right = nullptr;
}
}
return dummy->right;
}
};提示：很简单的中序遍历即可完成，这里采用的是迭代的写法，也可以使用递归的写法来完成。
相关推荐
2025-10-22
LeetCode刷题笔记(十二): 链表
算法介绍：链表是由节点和指针构成的数据结构，每个节点存有一个值，和一个指向下一个节点的指针，因此很多链表问题可以用递归来处理。不同于数组，链表并不能直接获取任意节点的值，必须要通过指针找到该节点后才能获取其值。同理，在未遍历到链表结尾时，我们也无法知道链表的长度，除非依赖其他数据结构储存长度。 代码实现：12345struct ListNode { int val; ListNode *next; ListNode(int x) : val(x), next(nullptr) {}}; 补充：由于在进行链表操作时，尤其是删除节点时，经常会因为对当前节点进行操作而导致内存或指针出现问题。有两个小技巧可以解决这个问题：一是尽量处理当前节点的下一个节点而非当前节点本身，二是建立一个虚拟节点(dummy...
2025-08-25
LeetCode刷题笔记(一): 贪心
贪心算法的核心思想：局部最优以实现全局最优。 一、分配问题 题目：分发糖果n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。你需要按照以下要求，给这些孩子分发糖果： 每个孩子至少分配到 1 个糖果。 相邻两个孩子中，评分更高的那个会获得更多的糖果。请你给每个孩子分发糖果，计算并返回需要准备的最少糖果数目。 解答： 123456789101112131415161718class Solution {public: int candy(vector<int> &ratings) { int n = ratings.size(); vector<int> candies(n, 1); for (int i = 1; i < n; ++i) { if (ratings[i] > ratings[i - 1]) { candies[i] = candies[i - 1] +...
2025-09-15
LeetCode刷题笔记(七): 数学问题
一、最大公约数和最小公倍数这个没什么好说的，辗转相除法： 1234567int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }int lcm(int a, int b) { return a * b / gcd(a, b); } 也可以通过扩展欧几里得算法(extended gcd)在求得a和b最大公因数的同时，也得到它们的系数x和y，从而使ax+by=gcd(a, b)，也就是贝祖等式。 12345678910int xGCD(int a, int b, int &x, int &y) { if (b == 0) { x = 1, y = 0; return a; } int x_inner, y_inner; int gcd = xGCD(b, a % b, x_inner, y_inner); x = y_inner, y =...
2025-08-27
LeetCode刷题笔记(三): 二分查找
二分查找算法的核心思想：二分查找也常被称为二分法或者折半查找 (binary search, bisect)，每次查找时通过将待查找的单调区间分成两部分并只取一部分继续查找，将查找的复杂度大大减少。对于一个长度为O(n)的数组，二分查找的时间复杂度为O(logn)。 一、求开方 题目：x 的平方根给定一个非负整数 x，求它的开方，向下取整。 解答： 12345678910111213141516int mySqrt(int x) { int l = 1, r = x, mid, x_div_mid; while (l <= r) { mid = l + (r - l) / 2; x_div_mid = x / mid; if (mid == x_div_mid) { return mid; } if (mid < x_div_mid) { l = mid + 1; }...
2025-09-18
LeetCode刷题笔记(八): 分治
算法解释：顾名思义，分治问题由“分”(divide)和“治”(conquer)两部分组成，通过把原问题分为子问题，再将子问题进行处理合并，从而实现对原问题的求解。我们在排序章节展示的归并排序就是典型的分治问题，其中“分”即为把大数组平均分成两个小数组，通过递归实现，最终我们会得到多个长度为1的子数组;“治”即为把已经排好序的两个小数组合成为一个排好序的大数组从长度为 1 的子数组开始，最终合成一个大数组。 自上而下的分治可以和 memoization 结合，避免重复遍历相同的子问题。如果方便推导，也可以换用自下而上的动态规划方法求解。 一、表达式问题 题目：为运算表达式设计优先级给定一个只包含加、减和乘法的数学表达式，求通过加括号可以得到多少种不同的结果。 解答： 1234567891011121314151617181920212223242526272829303132class Solution {public: vector<int> diffWaysToCompute(string expression) { ...
2025-08-26
LeetCode刷题笔记(二): 双指针
双指针算法的核心思想：双指针主要用于遍历数组，两个指针指向不同的元素，从而协同完成任务。也可以延伸到多个数组的多个指针。 一、Two Sum 题目：两数之和 II - 输入有序数组给你一个下标从1开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。 解答： 12345678910vector<int> twoSum(vector<int>& numbers, int target) { int l = 0, r = numbers.size() - 1, two_sum; while (l < r) { ...
评论
公告
去听サイエンス谢谢喵ヾ(=`ω´=)ノ”
