LeetCode刷题笔记(十四): 图

数据结构介绍：图通常分为有向(directed)或无向(undirected)，有循环(cyclic)或无循环(acyclic)，所有节点相连(connected)或不相连(disconnected)。树即是一个相连的无向无环图，而另一种很常见的图是有向无环图(Directed Acyclic Graph，DAG)。

补充：图通常有两种表示方法。假设图中一共有n个节点、m条边。第一种表示方法是邻接矩阵(adjacency matrix)：我们可以建立一个n×n的矩阵G，如果第i个节点连向第j个节点，则G[i][j]=1，反之为0；如果图是无向的，则这个矩阵一定是对称矩阵，即G[i][j]=G[j][i]。第二种表示方法是邻接链表(adjacency list)：我们可以建立一个大小为n的数组，每个位置i储存一个数组或者链表，表示第i个节点连向的其它节点。邻接矩阵空间开销比邻接链表大，但是邻接链表不支持快速查找i和j是否相连，因此两种表示方法可以根据题目需要适当选择。除此之外，我们也可以直接用一个m×2的矩阵储存所有的边。

一、二分图

算法解释：二分图算法也称为染色法，是一种广度优先搜索。如果可以用两种颜色对图中的节点进行着色，并且保证相邻的节点颜色不同，那么图为二分。

题目：判断二分图
给定一个图，判断其是否可以二分。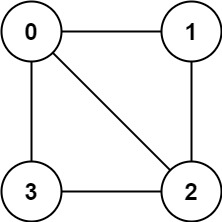
示例图

解答：

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        if (n == 0) return true;
        vector<int> color(n, 0); 
        queue<int> q;
        for (int start = 0; start < n; ++start) {
            if (color[start] != 0) continue;
            color[start] = 1;
            q.push(start);
            while (!q.empty()) {
                int u = q.front();
                q.pop();
                for (int v : graph[u]) {
                    if (color[v] == 0) {
                        color[v] = (color[u] == 1 ? 2 : 1);
                        q.push(v);
                    }
                    else if (color[v] == color[u])
                        return false;
                }
            }
        }
        return true;
    }
};

提示：首先使用广度优先搜索把所有相连的点都给标记上，这里有一个容易错的地方在于必须要遍历每一个点因为可能存在独立的点。

二、拓扑排序

算法解释：拓扑排序(topological sort)是一种常见的，对有向无环图排序的算法。给定有向无环图中的N个节点，我们把它们排序成一个线性序列；若原图中节点i指向节点j，则排序结果中i一定在j之前。拓扑排序的结果不是唯一的，只要满足以上条件即可。

题目：课程表 II
给定N个课程和这些课程的前置必修课，求可以一次性上完所有课的顺序。

解答：

class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> adjs(numCourses);
        vector<int> degrees(numCourses);
        for (auto& v : prerequisites) {
            adjs[v[1]].push_back(v[0]);
            ++degrees[v[0]];
        }
        queue<int> q;
        vector<int> res;
        for (int i = 0; i < numCourses; ++i)
            if (degrees[i] == 0) q.push(i);
        while (!q.empty()) {
            int size = q.size();
            while (size--) {
                int index = q.front();
                q.pop();
                res.push_back(index);
                auto &adj = adjs[index];
                for (auto& it : adj) {
                    --degrees[it];
                    if (!degrees[it]) q.push(it);
                }
            }
        }
        if (res.size() < numCourses) return {};
        return res;
    }
};

提示：拓扑排序也可以被看成是广度优先搜索的一种情况：我们先遍历一遍所有节点，把入度为0的节点(即没有前置课程要求)放在队列中。在每次从队列中获得节点时，我们将该节点放在目前排序的末尾，并且把它指向的课程的入度各减1；如果在这个过程中有课程的所有前置必修课都已修完(即入度为0)，我们把这个节点加入队列中。当队列的节点都被处理完时，说明所有的节点都已排好序，或因图中存在循环而无法上完所有课程。

三、练习

因为LeetCode要会员以及图论相关的题本就不多的原因，这里的图论算法只涉及到Dijkstra无负边单源最短路算法。还有Kruskal’s Algorithm和Prim’s Algorithm最小生成树算法，最小流算法，Bellman-Ford单源最短路算法以及Floyd-Warshall算法等需要掌握。

题目：细分图中的可到达节点
给你一个无向图(原始图)，图中有n个节点，编号从0到n-1。你决定将图中的每条边细分为一条节点链，每条边之间的新节点数各不相同。要细分边[ui, vi]，需要将其替换为(cnti + 1) 条新边，和cnti个新节点。新节点为x1,x2,…,xcnti，新边为[ui, x1],[x1, x2],[x2, x3],…,[xcnti-1, xcnti],[xcnti, vi]。
示例图

class Solution {
public:
    int reachableNodes(vector<vector<int>>& edges, int maxMoves, int n) {
        vector<vector<pair<int, int>>> adjs(n);
        for (auto& edge : edges) {
            adjs[edge[0]].push_back({edge[1], edge[2] + 1});
            adjs[edge[1]].push_back({edge[0], edge[2] + 1});
        }
        vector<int> dist(n, __INT_MAX__);
        dist[0] = 0;
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
        pq.emplace(0, 0);
        while (!pq.empty() && pq.top().first < maxMoves) {
            auto [dis, u] = pq.top();
            pq.pop();
            if (dis > dist[u]) continue;
            for (auto& [v, cnt] : adjs[u]) {
                int newDis = cnt + dis;
                if (newDis < dist[v]) {
                    dist[v] = newDis;
                    pq.emplace(newDis, v);
                }
            }
        }
        int sum = 0;
        for (int& dis : dist) {
            if (dis <= maxMoves) ++sum;
        }
        for (auto& edge : edges) {
            int x = max(maxMoves - dist[edge[0]], 0);
            int y = max(maxMoves - dist[edge[1]], 0);
            sum += min(edge[2], x + y);
        }
        return sum;
    }
};